1. Compare and contrast closeness centrality and betweeness centrality. Explain the significance of betweeness centrality measure and focus on at least two applications.
2. How would you correlate page rank algorithm with random surfer algorithm and markov chain problem?
3. For the following web graph calculate page rank and hubs and authority score .
 |
Write all steps in matrix construction and up to two iterations write intermediate steps using manual calculation. After five iterations write final scores.
4. In a very general way how would you explain the notion of an authority pages and hub pages.
Give 5 examples of web pages (URLs) which you think are good authority and hub pages . Try that examples are mutually related. Focusing on its inlinks and outlinks of pages , justify wrt HITS why do you consider that these are good authority (hub) pages.
5. Explain how you can use co citation and co reference as similarity measure for finding similarity between two nodes in a graph.
Give a proper example taking a graph and various pair of nodes and justify how to nodes are similar and how two nodes are distant w.r.t. these two measures.
1. Compare and contrast closeness centrality and betweeness centrality. Explain the significance of betweeness centrality measure and focus on at least two applications.
Answer:
Comparison between Closeness Centrality and Betweenness Centrality:
- Closeness Centrality measures that how easily any actor (node) in a social network can interact with all other actors. This is based on the closeness and closeness can be measured using distance. Whereas the betweennes centrality measures that if any actor (node) is on the path between two actors then how much it can control over the interaction of these actors.
- The shortest distance between the two actors is used to measure the closeness centrality whereas the number of shortest distance between the two actors are used to measure the betweenness centrality.
- Closeness centrality can be computed for only the connected graph but betweenness centrality can be calculated for both connected and disconnected graphs. Both centralities can be computed for directed and undirected graphs.
- In closeness centrality same equation can be used for both directed and undirected graphs whereas in standardized betweenness centrality there is variation in equation for directed and undirected graphs. For directed graphs the standardized betweenness centrality is two times that of for the undirected graphs.
Significance Of Betweenness Centrality:
The betweenness Centrality is very significant in analyzing Network. Network may our social network like twitter or facebook or may be some different type of network like network of cancer diagnosis. Betweenness Centrality is widely used measure that captures a person's role in allowing information to pass from one part of the netwotk to the other.
A node in social network with high betweenness is likely to be aware of what is going in multiple social circles. For example consider a Twitter account. It captures how important a node is in flow of information from one part of the network to another. Between can have many meanings. One meaning may be that a user with high betweenness may be followed by many others who don't follow the same people as the user. This can indicate that the user well followed. Other way the user may have fewer followers, but connect them to many accounts that are otherwise distant. This would indicate the user is reader of many people.
2. How would you correlate page rank algorithm with random surfer algorithm and Markov chain problem?
Answer:
The Page Rank algorithm based on the rank prestige can be find as the principal eigenvector of the characteristic equation P = ATP. In this characteristic equation Page rank vector P is an eigenvector with corresponding eigenvalue of 1. But the above characteristic equation does not satisfy all the conditions so as we can find the principal eigenvector. To overcome these problems we use Markov chain to find the same equation so that we can derive the Page Rank vector.
In Markov chain model the web page or node in the web graph regarded as a state. A hyperlink as transition, which leads from one state to the other state with some probability. In this model the web surfing is treated as a stochastic process. This incorporate random surfer algorithm that state any web surfer at initial state can surf randomly with some probability any page out linked this page. Suppose any user is at some page (state in Markov chain model). This page has many out links (hyperlinks). These hyperlinks are as transition. The user can click the links randomly with some initial probability. Sum of these probabilities p(1), p(2),..., p(n) for a user is 1. We have the transition probability matrix A. This is a n x n matrix for n states(pages). Entries in this matrix are one divided by the total hyperlinks (out links) in the page. This matrix A is a stochastic Matrix of Markov chain if the sum of each row is equal to 1. In Markov chain model the next state can be calculated from the current state with the equation pk = AT pk-1. After a series of transition pk will converge to a steady state probability vector. This steady state probability is the principal eigenvector wit eigenvalue of 1. In this page rank algorithm this steady state probability vector is used as the page rank vector.
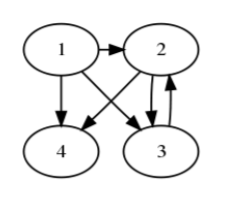
3. For the following web graph calculate page rank and hubs and authority score .
Write all steps in matrix construction and up to two iterations write intermediate steps using manual calculation. After five iterations write final scores.
Code the algorithm and test the results for different initial conditions. Comment on the result.
Answer:
Page Rank Calculation:
To find the state transition probability matrix we have assumption that a random surfer will click the link with uniform probability. Here page 1 have 3 links so surfer will click any link uniformly with 1/3. So in first row entry for A12, A13, A14 will be 1/3 each. So that row sum is 1. Similarly in second row A23, A24 will be 1/2 each, other entries are zero because no link to those nodes. Similarly for 3rd row the entries are 0,1,0,0 and in 4th row the entries are all zeroes.
The state transition probability matrix for the above graph:
This matrix is not an stochastic matrix because all entries in 4th row are zero. So to make the matrix stochastic we will add a link from node 4 to every node. Hence now the state transition probability matrix is as below:

Now our graph is irreducible because now the graph is strongly connected ie. there is a path between any pair of the nodes.
Let initial probability vector be P will be
1st Iteration:
2nd Iteration:

Hubs and Authority Scores
Calculation:
The Adjacency Matrix for above graph
Let the starting condition for hubs and authority as follows:
Authority score calculation
1st Iteration:
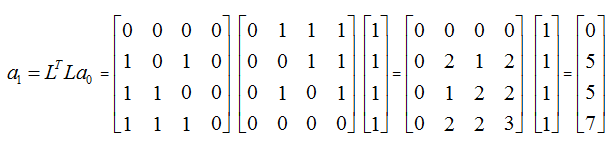
After Normalization
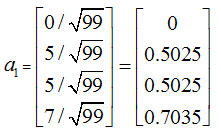
2nd Iteration:
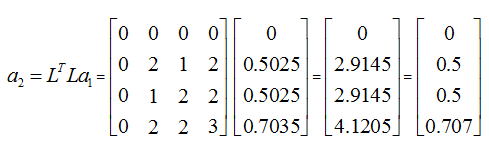
After 5 iterations the Authority score
Hub score calculation
1st Iteration:
After Normalization
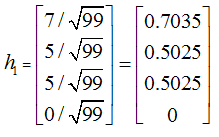
2nd Iteration:
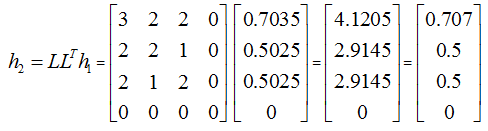
After 5 iterations Hub Score
4. In a very general way how
would you explain the notion of an authority pages and hub pages.
Give 5 examples of web pages (URLs) which you think are good authority and hub pages .
Try that examples are mutually related. Focusing on its inlinks and outlinks of
pages , justify wrt HITS why do you consider that these are good authority
(hub) pages.
Answer: A web page is said to be an authority page if it has many in-links. And a web page is a hub page if it has many out-links. A good authority page is that which is trusted by many people on a particular topic and they link it. A good hub page is that which has lots of information about the topic and links to good authority pages. So a good authority page on a particular topic is linked by many good hubs and a good hub page links many good authority pages on a particular pages. Example of an authority is web page our university it has in-links from many good hub pages like ugc, nirf, hrd etc if we search for higher education.
5 Examples of good authority pages:
5 Examples of good hub pages
1. https://www.iitsystem.ac.in/
2. https://en.wikipedia.org/wiki/Indian_Institutes_of_Technology
4. https://www.iitkgpfoundation.org/
These examples are mutually related because if we search for iit the good hub pages are the above. These hub pages gives best link to find the appropriate information about the iit. And the authority pages are best pages to find the information related to particular iit and these pages are pointed by the good hub pages. For iit delhi the best page to get the information is the iit delhi official web page www.iitd.ernet.in, most authoritative page and like for all iits. And the hub pages are the best pages to point to these all iit web sites. So these examples are mutually related.
The HITS consider the best 200 pages in the root set and the in base set more pages for each page in root set. Then assigns authority score and hub score. Then return the best pages with these scores. If an authority is good authority page then its score will be more and any authority page is good if it is pointed by good hub pages. In our examples the HITS algorithm work well because these are the examples of good authority and hub pages so these will score good score while HITS scoring the authority and hub scores.
5. Explain how you can use co
citation and co reference as similarity measure for finding similarity between
two nodes in a graph.
Give a proper example taking a
graph and various pair of nodes and justify how to nodes are similar and how
two nodes are distant w.r.t. these two measures.
Answer: The co-citation is used to find the similarity between two papers. when two papers a cited by same papers then we say that these two papers are somehow related or similar. The co-citation can be used to find the similarity between the two nodes in a graph. The graph must be a directed graph. If two nodes are pointed by some same nodes then these two nodes will be similar. If these nodes are more similar if they are pointed by many nodes.
Co-reference is also used to find the similarity between two papers. When two papers are citing same papers then these two papers are somehow related or similar to each other. The co-reference can be used to find the similarity between two nodes in the directed graph. If any two nodes are pointing to same nodes then they are similar to each other. If they are pointing more same nodes they will be more similar.
Let the below example graph:
First we consider Co-citation for finding similarity between pair of nodes in the above graph.
Nodes (2,3) are similar because both nodes are pointed (cited) by same node 1. Nodes(1,3) are similar because they both are pointed (cited) by node 2. Nodes (5, 6) are cited by node 4 and nodes (4,5) are cited by the node6, nodes (3,5) cited by node 4. so they are similar. Nodes (3,4) is a best example of the nodes that are distant with respect to co-citation and co-reference. Other Distant nodes pair are (1,5), (2,5), (1,6), (2,6), (1,4).
Now consider Co-reference for finding similarity between pair of nodes in the above graph.
Nodes (1,2) are similar because they both are citing or referencing (pointing) same node 3. Similarly nodes (1,3) are referencing node 2 so they are similar. Nodes (1,4) are similar both referencing node3. Nodes (2,4) are similar both citing node 3. Nodes (4,6) are similar both citing node 5. Nodes (1,5), (1,6), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5) are distant nodes pair.
Useful Resources:
Previous Post:Web Mining: Important Questions and Answers on Information Retrieval (IR)

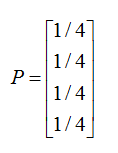


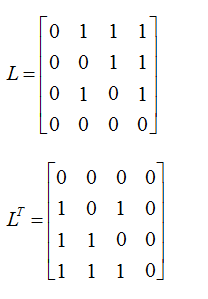


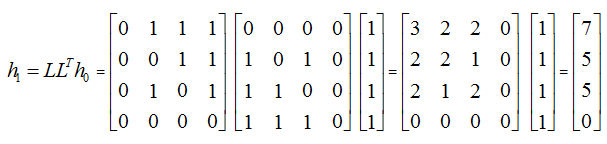
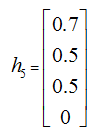

Comments
Post a Comment